Decimal to binary
This converter can convert decimal numbers to binary numbers very quickly, both negative and floating-point numbers are supported for conversion. At the same time, you can also choose any conversion between binary to base 36. Binary to decimal
| Base(default decimal) | |
| Decimal number | |
| Target base(default binary) | |
| Conversion result |
Knowledge of converter
In mathematics and digital electronics, a binary number is a number expressed in the base-2 numeral system or binary numeral system, which uses only two symbols: typically 0 (zero) and 1 (one).
The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices.
How to convert decimal to binary
- Divide the number by 2.
- Get the integer quotient for the next iteration.
- Get the remainder for the binary digit.
- Repeat the steps until the quotient is equal to 0.
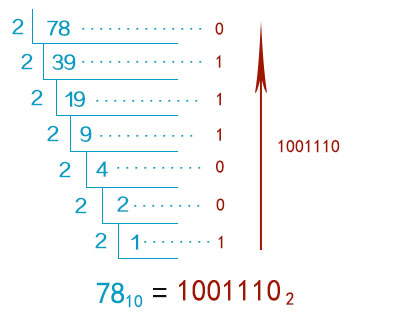
Example
Convert 1510 to binary:
| Division by 2 | Quotient | Remainder | Bit # |
|---|---|---|---|
| 15/2 | 7 | 1 | 0 |
| 7/2 | 3 | 1 | 1 |
| 3/2 | 1 | 1 | 2 |
| 1/2 | 0 | 1 | 3 |
So 1510 = 11112
Decimal to binary conversion table
| Decimal Number | Binary Number |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
| 21 | 10101 |
| 22 | 10110 |
| 23 | 10111 |
| 24 | 11000 |
| 25 | 11001 |
| 26 | 11010 |
| 27 | 11011 |
| 28 | 11100 |
| 29 | 11101 |
| 30 | 11110 |
| 31 | 11111 |
| 32 | 100000 |
| 64 | 1000000 |
| 128 | 10000000 |
| 256 | 100000000 |